Если в двузначной логике высказывания (суждения) делятся на истинные и ложные, то в дедуктивных системах формулы делятся на доказанные и недоказанные. Разница существенна. Если я скажу, что ровно через год после чтения этих слов вы получите денежный приз, это заявление не будет ложным, поскольку по случайности какой-нибудь приз вы можете получить. С другой стороны, это заявление не будет и истинным, поскольку никакого приза может и не быть. Понятно, что я не пророк, и подобные вещи предсказывать не могу. Поэтому мое заявление и не ложно, и не истинно,- оно не доказано. И я в этот момент и не лгу, не говорю правду, а делаю, что называется, "необоснованное заявление".
Идея любой дедуктивной системы состоит в том, чтобы доказать хотя бы некоторые из формул на основе других, уже доказанных формул. Таким образом, новые доказанные суждения получаются из ранее доказанных суждений. В таком случае надо с чего-то начать. Начинать полагается с аксиом.
 [правила построения аксиом]: Правила построения аксиом - это строгие правила,
позволяющие построить некоторые формулы данной (и только данной) дедуктивной системы.
[правила построения аксиом]: Правила построения аксиом - это строгие правила,
позволяющие построить некоторые формулы данной (и только данной) дедуктивной системы.
 [аксиома]: Формула дедуктивной системы получает звание "аксиома",
если ее можно получить с помощью правил построения аксиом.
[аксиома]: Формула дедуктивной системы получает звание "аксиома",
если ее можно получить с помощью правил построения аксиом.
Количество аксиом, в принципе, может быть бесконечным. Если количество аксиом конечно, то правила построения аксиом можно написать в виде простого перечисления. Если количество аксиом бесконечно, тогда необходимо задать какие-нибудь другие строгие правила. Обычно они очень примитивны и недалеко уходят от простого перечисления. Например, это могут быть так называемые "схемы аксиом" - формулы с переменными, на место которых могут быть подставлены определенные символы.
 [правила вывода]: Правила вывода - это строгие правила, по которым
от одной или нескольких формул дедуктивной системы можно перейти к одной
или нескольким формулам той же дедуктивной системы (обычно это будут уже другие формулы).
[правила вывода]: Правила вывода - это строгие правила, по которым
от одной или нескольких формул дедуктивной системы можно перейти к одной
или нескольким формулам той же дедуктивной системы (обычно это будут уже другие формулы).
 [дедуктивный переход]:
[дедуктивный переход]:
 [шаг дедукции]:
[шаг дедукции]:
 [дедуктивный шаг]: Дедуктивный переход (дедуктивный шаг, шаг дедукции)
- это однократный переход от некоторой совокупности формул к другой совокупности формул согласно правилам вывода.
[дедуктивный шаг]: Дедуктивный переход (дедуктивный шаг, шаг дедукции)
- это однократный переход от некоторой совокупности формул к другой совокупности формул согласно правилам вывода.
Количество формул, с которыми имеют дело правила вывода в течении одного шага дедукции должно быть конечно, ведь наш эталон строгости (персоналка) не может обработать бесконечно большое количество текста.
Итак, в любой ДС есть три группы строгих правил:
- Правила построения формул, позволяющие отличить формулу данной ДС от любой другой строки текста.
- Правила построения аксиом, позволяющие отличить аксиому данной ДС от любой другой формулы данной ДС.
- Правила вывода, позволяющие перейти от одних формул данной ДС к другим.
Будем записывать шаг дедукции в следующем формате:
Здесь:
Насчет формы записи дедуктивного шага. Этот вариант не является общепринятым. Чаще
используют два других. В одном случае пишут исходный набор формул, проводят длинную
горизонтальную черту, а под ней пишут полученный набор формул. Получается что-то вроде
дроби:
Я не использую эту запись не столько потому, что ее можно спутать с арифметической
дробью, сколько потому, что дроби неудобно записывать в компьютерных текстах, а символ
Такой вариант записи кажется проще, но только до тех пор, пока мы не попытаемся понять, из
каких формул следует очередная формула. Чтобы не гадать, приходится добавлять комментарий,
где для каждой полученной формулы указываются исходные формулы и правило вывода. Если
строго регламентировать вид этого комментария, то формула вместе с комментарием как раз
и составит что-то вроде нашей записи (1).
Все варианты оформления шагов дедукции взаимозаменяемы. В конце главы буден приведен еще
один вариант (в виде графа).
Количество формул слева от
В дедуктивной системе есть два "звания" для формул: "аксиома" и "теорема".
Формула получает звание "аксиома", если ее можно получить с помощью правил
построения аксиом. Остальные формулы могут получить звание "теорема". Для
этого надо найти дедуктивный шаг вида (1), в котором все формулы слева
от
Здесь мы еще раз видим различие между истинностью и доказанностью. Любая аксиома есть
по определению доказанная формула. Однако мы можем объявить аксиомой любую формулу,
в том числе и заведомо бредовую. Такая аксиома будет доказанной (в рамках этой ДС),
но не будет истинной.
Таким образом, в ДС доказанной считаются во-первых, все аксиомы - просто потому, что
они получены с помощью правил построения аксиом и, во-вторых, все формулы, которые
получаются из ранее доказанных формул с помощью правил вывода. Процесс
присвоения гордого звания "теорема" все новым формулам как раз и называется
"доказательством" (по крайней мере в контексте разговора о дедуктивных системах).
Например, пусть есть три аксиомы
Вы видите, как некоторая формула-теорема
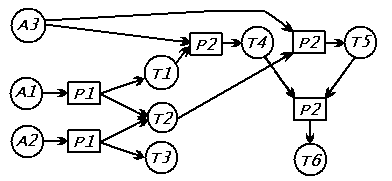
Можно нарисовать схему, в которой узлами являются формулы и правила вывода,
а линии показывают дедуктивные шаги. В нашем примере схема выглядит так:
Итак, если говорить формально, то в понятие дедуктивной ссистемы входят следующие составляющие:
алфавит, правила построения формул, правила построения аксиом, правила вывода и все формулы.
 G1, G2,..., GM // R
G1, G2,..., GM // R





 [теорема]: Формула, которая не является аксиомой, получает звание
"теорема", когда обнаруживается шаг дедукции от группы формул, каждая из
которых уже получила ранее звание, к другой группе формул, в которую входит
данная формула.
[теорема]: Формула, которая не является аксиомой, получает звание
"теорема", когда обнаруживается шаг дедукции от группы формул, каждая из
которых уже получила ранее звание, к другой группе формул, в которую входит
данная формула.
 [доказанная формула]: Формула называется доказанной, если она уже
получила к данному моменту звание "аксиомы" или "теоремы".
[доказанная формула]: Формула называется доказанной, если она уже
получила к данному моменту звание "аксиомы" или "теоремы".
 [декукция]:
[декукция]:
 [дедуктивное доказательство]:
[дедуктивное доказательство]:
 [дедуктивный вывод]: дедукцией или дедуктивным доказательством
или дедуктивным выводом будем называть текст, в котором перечислены один или несколько
дедуктивных шагов, в результате которых хотя бы одна формула получает звание "теоремы".
[дедуктивный вывод]: дедукцией или дедуктивным доказательством
или дедуктивным выводом будем называть текст, в котором перечислены один или несколько
дедуктивных шагов, в результате которых хотя бы одна формула получает звание "теоремы".
 T1, T2 // P1
T1, T2 // P1 T4 // P2
T4 // P2 T3, T2 // P1
T3, T2 // P1 T5 // P2
T5 // P2 T6 // P2
T6 // P2